数学建模问题
龙虾数量与利润预测分析
1. 数据概览
| 年份 | 龙虾数量 (万只) | 每只龙虾成本 (元) | 每只龙虾售价 (元) |
|---|---|---|---|
| 1 | 3.81 | 0.55 | 4.15 |
| 2 | 3.92 | 0.58 | 4.18 |
| 3 | 3.95 | 0.62 | 4.32 |
| 4 | 4.02 | 0.67 | 4.34 |
| 5 | 4.10 | 0.71 | 4.43 |
| 6 | 4.13 | 0.74 | 4.57 |
| 7 | 4.16 | 0.76 | 4.63 |
| 8 | 4.17 | 0.81 | 4.76 |
| 9 | 4.26 | 0.83 | 4.86 |
| 10 | 4.39 | 0.87 | 4.94 |
| 11 | 4.58 | 0.91 | 5.06 |
| 12 | 4.83 | 0.92 | 5.11 |
| 13 | 4.98 | 0.95 | 5.26 |
| 14 | 5.07 | 0.99 | 5.39 |
| 15 | 5.17 | 1.02 | 5.49 |
| 16 | 5.30 | 1.05 | 5.52 |
| 17 | 5.39 | 1.08 | 5.66 |
| 18 | 5.46 | 1.10 | 5.77 |
| 19 | 5.53 | 1.13 | 5.92 |
| 20 | 5.60 | 1.15 | 6.03 |
2. 模型概述
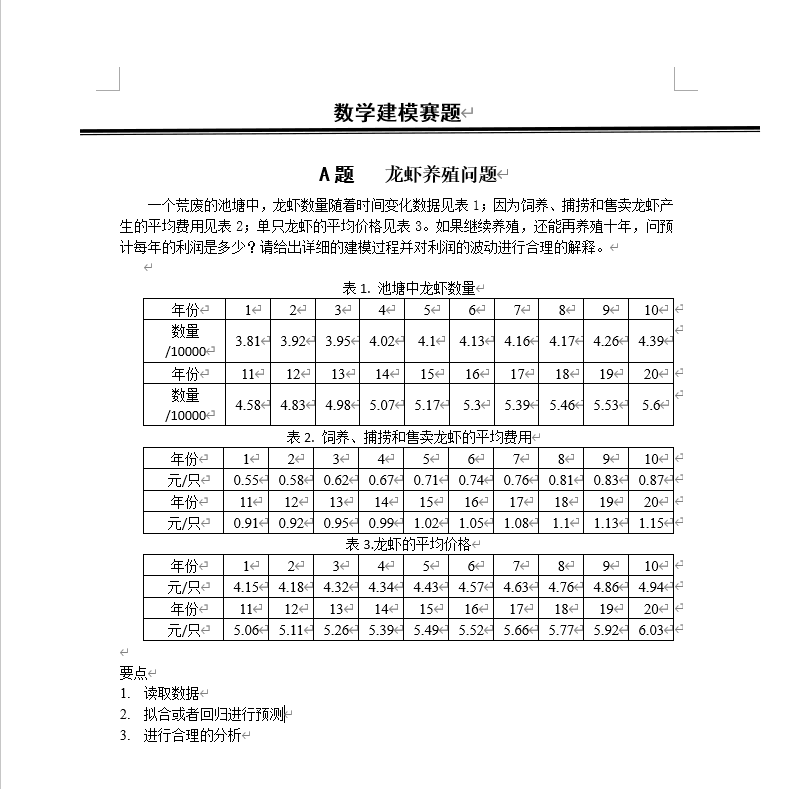
2.1 逻辑斯蒂模型:预测龙虾数量
使用逻辑斯蒂模型拟合历史龙虾数量数据,模型公式如下:
[
Q(t) = \frac{K}{1 + a \cdot e^{-r \cdot t}}
]
其中:
- ( Q(t) ) 为第 t 年的龙虾数量(单位:万只)
- ( K ) 为最大龙虾数量(拟合参数)
- ( r ) 为增长速率(拟合参数)
- ( a ) 为模型常数(拟合参数)
通过对历史数据的拟合,得到的参数为:
- ( K = 6.68 )
- ( r = 0.134 )
- ( a = 1.034 )
使用该模型,预测未来 10 年(即 21 年到 30 年)的龙虾数量。
2.2 线性回归模型:预测成本与售价
分别使用线性回归模型拟合每只龙虾的成本和售价:
- 成本模型:( C(t) = a \cdot t + b )
- 售价模型:( P(t) = a \cdot t + b )
通过拟合历史数据,得到的参数如下:
- 成本回归模型:( C(t) = 0.0218 \cdot t + 0.5172 )
- 售价回归模型:( P(t) = 0.0539 \cdot t + 3.9948 )
2.3 利润计算
根据未来 10 年的龙虾数量、成本和售价,计算每年的利润:
[
\text{Profit} = (P(t) - C(t)) \cdot Q(t) \cdot 10^4
]
单位:万元
3. 未来 10 年的预测结果
3.1 预计龙虾数量
| 年份 | 预计龙虾数量 (万只) |
|---|---|
| 21 | 5.69 |
| 22 | 5.77 |
| 23 | 5.84 |
| 24 | 5.92 |
| 25 | 5.99 |
| 26 | 6.07 |
| 27 | 6.14 |
| 28 | 6.21 |
| 29 | 6.28 |
| 30 | 6.34 |
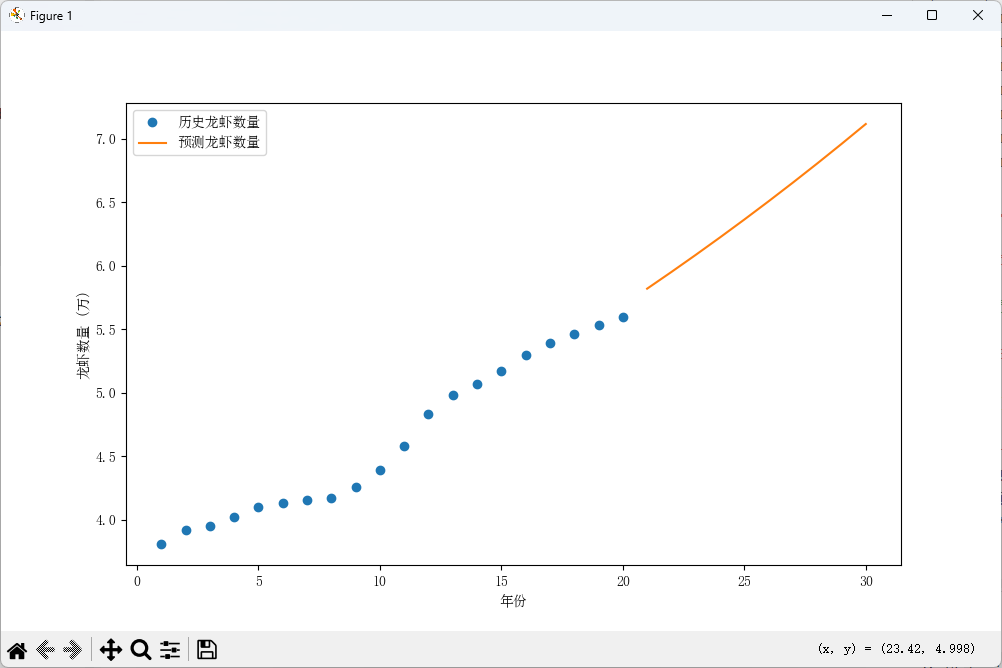
3.2 预计利润
| 年份 | 预计利润 (万元) |
|---|---|
| 21 | 124.13 |
| 22 | 129.43 |
| 23 | 134.80 |
| 24 | 140.14 |
| 25 | 145.42 |
| 26 | 150.66 |
| 27 | 155.85 |
| 28 | 160.97 |
| 29 | 165.97 |
| 30 | 170.84 |
4. 可视化结果
4.1 未来 10 年的利润预测
5. 结论与建议
- 龙虾数量:根据逻辑斯蒂模型预测,未来 10 年内龙虾数量将保持增长,预计会趋于饱和,在 30 年时达到约 6.34 万只。
- 利润预测:基于成本与售价的线性回归模型,未来 10 年的利润呈稳步上升趋势,预计最高利润将接近 170 万元。
- 建议:考虑到龙虾数量和利润的持续增长,建议进一步优化成本控制和销售策略,以提高整体盈利能力。

1 条评论
滴!学生卡!打卡时间:13:31:42,请上车的乘客系好安全带~